Little Arithmetic Master
If the game cannot run in the web page, you can download here:
download:https://pan.baidu.com/s/1NQEybfBphaEakYPbd0J1AA
password:4vg9
Need
Specific Need
Nowadays, many primary school students are relying so heavily on using calculators for them to calculate basic arithmetic problems (Sun, 2004). In fact, I don't mean students cannot use calculators anymore, the author and I hope students can use calculators to calculate complex arithmetic problems. One of the most serious problems for using too many calculators or other tools in primary school is students will not think deeply about how they can make complex calculations easier. It seems like this is not a problem but I think building a habit of thinking logically is more important than getting straight the results. Basic calculation is a kind of tool to train basic logic skills, so students from all over the world need it and students should use their thoughts to come up with some ideas to make complex arithmetic questions easier to solve.
In conclusion, this specific need is to train students to think deeply and come up with some ideas to make complex calculations easier.
Related to education
This need is related to education, especially in the area of mathematics. Moreover, making calculation easier not only means we can get the result quicker, but also mean the students use their thoughts to make a complex thing easier. This is what I mean thinking deeply.
Need is real with literature
Based on the article Make simple calculations more "simple", simple calculations in elementary school are a difficult point for students to learn. Make complex calculations become easier is the most flexible type of calculation question. It can fully exercise the flexibility of students' thinking and play an important role in improving students' calculation ability. It is not an easy task to effectively implement simple calculation teaching and let students master simple calculations. For this reason, we must break through this difficulty in teaching (Zhang, 2016). Based on the article Disadvantages and Countermeasures of Using Calculators for Primary School Students, the calculator can help to solve complex and difficult questions but if primary school students get used to overusing it, they will become think less and it's bad for their logic skills improvement (Sun, 2004). I search from google and other books and find one which can teach some skills to make complex calculations easier (Sticker, 1955).
https://www.ixueshu.com/document/bf2179acdc574e56318947a18e7f9386.html
https://wenku.baidu.com/view/9ef15b34872458fb770bf78a6529647d272834f1.html
https://books.google.com.hk/books?hl=zh-CN&lr=&id=wnhc0-EKaGYC&oi=fnd&pg=PP1&dq=...
users and context
The users are the students before grade 3 and the context is the primary school that wants to train their students to think critically and logically. Especially, the context mainly focuses on the students who are before grade 3.
Design Description
description of the design with images
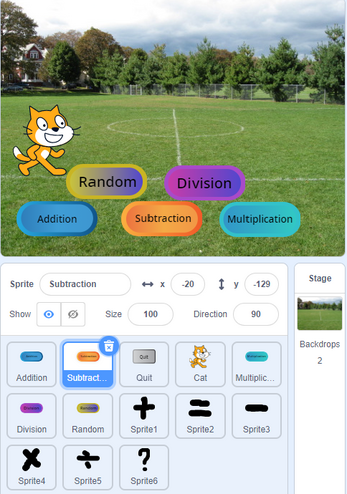
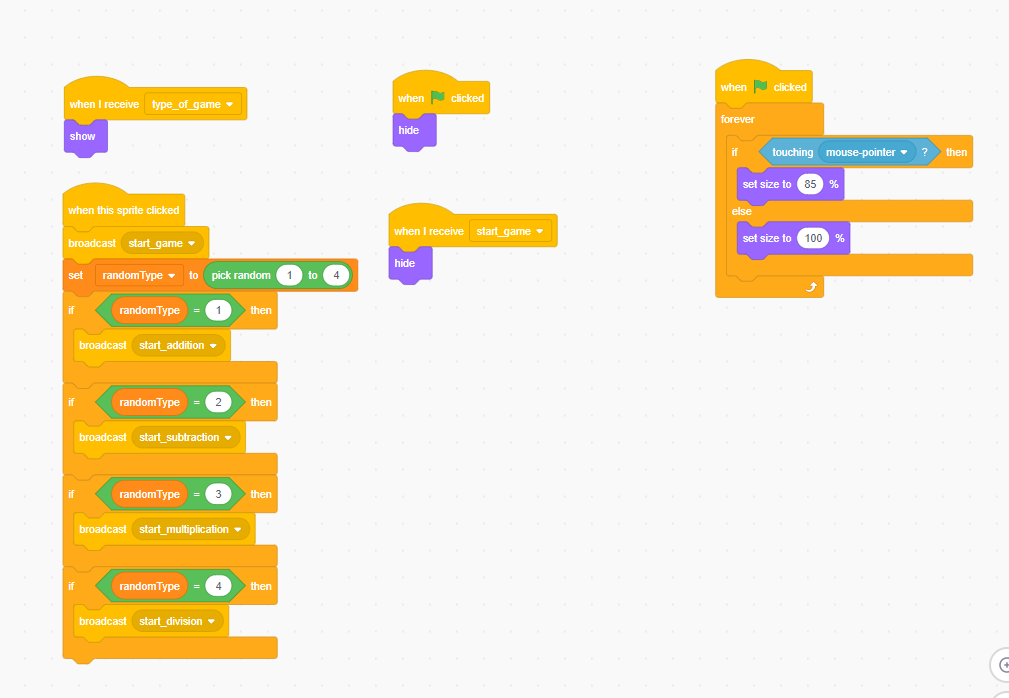
For designing this educational game, I use scratch 3.0. My idea is to use direct UI including options for choosing different arithmetic training modes. Also, I add a cat to make the game become more interesting and appeal to students. The game will also provide two temp variables for students which can record the two numbers that they want to use to replace the original second addend or subtrahend or multiplier or divisor. I aim to let the students think up two numbers that can use them to separate the original calculation way and make the calculation easier (center, 2020). When I design addition, subtraction, and multiplication, I use Associative laws, Distributive Laws with some ideas from Henry's book, How to Calculate Quickly: The Art of Calculation (Sticker, 1955). For division, I just use Associative laws. The general idea is to let the students find any combinations of different two numbers that can let one-step calculation become two steps calculation. Although the steps increase, the calculation will become easier. There is no standard answer about how you choose the two numbers but this what I want from the students that they can try different numbers in different situations and try their best to come up with some numbers which can make the calculation easier. For the core code of the project, I nearly use all kinds of blocks in scratch 3.0. I design 4 functions for arithmetic calculation, and two functions for implementation of making calculation easier.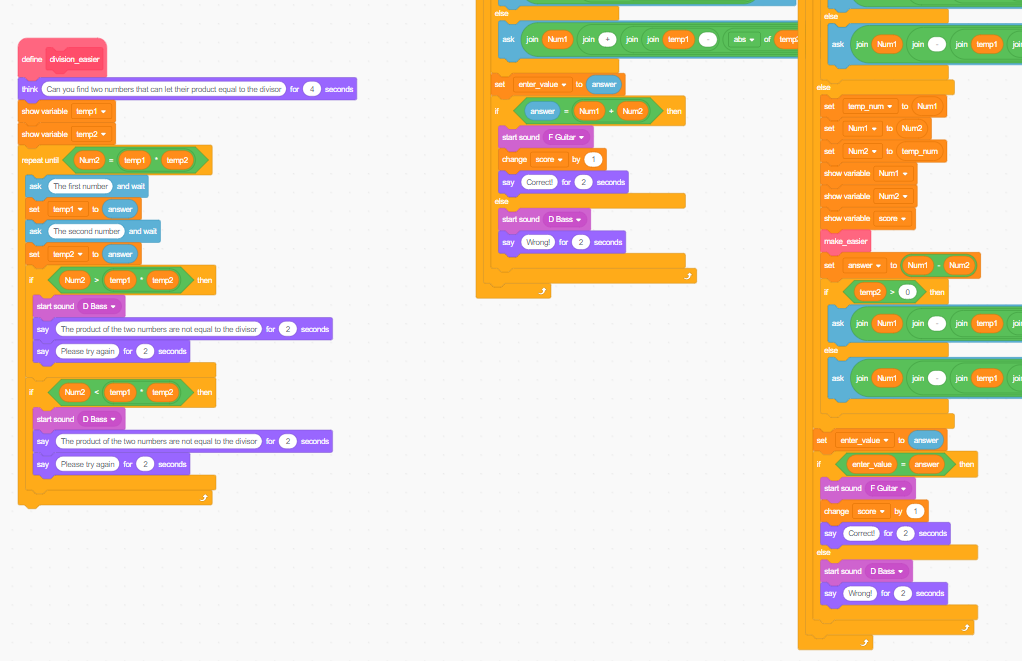
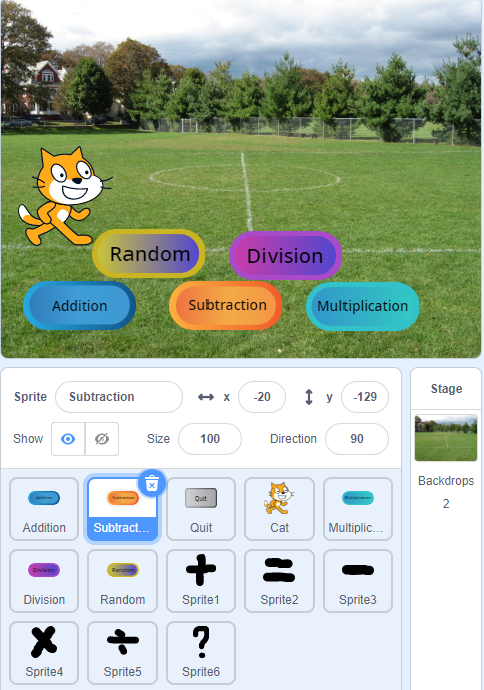

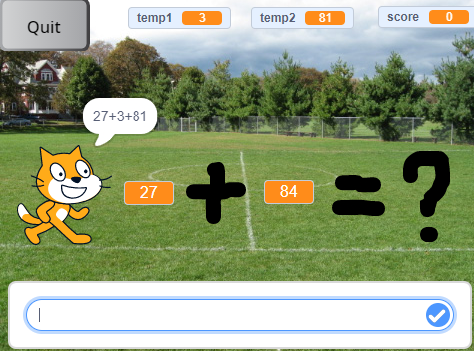
game mechanics
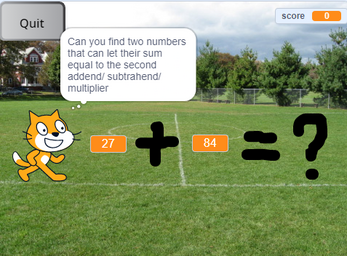
Rules: players start the game and choose what kind of arithmetic training that they want to do: random, addition, subtraction, multiplication, or division. After that, the game will randomly generate two numbers and ask the players to think up another two numbers which can be added together to replace the second addend/ subtrahend/ multiplier (for addition, subtraction and multiplication). For division, the players should think up two numbers and let them multiply each other to replace the second divisor. There is no standard answer, so what the players need to is to try their best to get the most suitable combination of the two numbers. Then the cat will show the new formula, and players just use the new formula to get the correct answer.
Data expressions: the temp numbers for replacing the second addend/ subtrahend/ multiplier/ divisor will be shown at the top of the game. One variable called score will calculate how many correct answers that the players get. Three input boxes for inputting the number. If the answer is correct, the sound of the guitar will be played. If the answer is not correct, the sound of the bass will be played.
Algorithms:
The score will be added by one if the answer is correct; different numbers will be generated by using the block of random.
How game support learning
Based on my design description and the mechanics, the players should think up another two numbers which can be added together to replace the second addend/ subtrahend/ multiplier (for addition, subtraction and multiplication). For division, the players should think up two numbers and let them multiply each other to replace the second divisor. This game focuses on the procedures of thinking up the combinations of two numbers. Different numbers will make the calculation easier or even more difficult. For example, one easy way is to get two numbers that can make the first addend add one of the two numbers to create an integer, then add the rest of the number. Each time when the players type the two temp numbers, they will be recorded and the new formula will be shown at once. Players can use the new formula to calculate. The game can improve the logic skills of players by pushing players to think up the numbers to make the calculation easier.
Dynamics
Challenge:
The numbers are generated randomly, so the players can experience different levels of questions, and they may get the challenging question and think more. For addition, subtraction and multiplication, the players should consider the combinations of two numbers' sum. For division, they should consider the product.
Expression:
The score will be expressed by the points, the total of the points means how many correct answers the player gets. Players can decide which temp number to use, so they can change the question to become easier or even harder.
Interactions:
Players use the mouse and the keyboard to type the number. When they get the correct answer they will hear the sound of the guitar and if they get the wrong answer they will hear the sound of bass.
Aesthetics
Sensation
the visualization of the game is clear. The formula and symbol will be changed when the user types the temp numbers. So, it's convenient for users to know whether their idea can make the calculation easier or not.
Challenge
Random numbers and make division easier may be the hardest one for players.
Expression
Players use their ideas to generate temp numbers and test whether their thoughts can make the calculation easier or not.
Submission:
When the player thinks up the numbers, they just make good use of their time and they think logically.
successes and challenges of the design process
success:
The logic of calculation is developed successfully. For two functions of making calculation easier, they are also successful. I think the procedures for thinking up the combinations of different numbers can be implemented because I have a good guide for them, such as prompting the players to type the number one by one, when they type the number, they must think about whether the number is suitable that can let the calculation become easier. After they typing, they can also see the new formula that they create.
challenge:
The harder part is developing division. Because the audience is the students who are before grade 3, they haven't touched the knowledge about fraction numbers. To not let the fraction number show in my game, I do one more loop to firstly make the first divisor is always larger or equal to the second divisor.
References
center, o. m. (2020). ALGEBRA LAWS: Commutative, Associative, Distributive Laws. Retrieved from whatcom: https://www.whatcom.edu/home/showpublisheddocument?id=1702
Sticker, H. (1955). How to Calculate Quickly: The Art of Calculation. Uni: Dover Publications.
Sun, L. (2004). Disadvantages and Countermeasures of Using Calculators for Primary School Students. Primary school teaching reference: Mathematics, 88-89.
Zhang, Q. (2016). Make simple calculations more "simple". Educational Science (Full Text Edition), 140-140.
| Status | Released |
| Platforms | HTML5 |
| Author | jy3084 |
| Genre | Educational |
| Tags | 2D, Singleplayer |